馬場茂雄
　
根本特殊化学ライフサイエンス研究所
300-2521　茨城県水海道市大生郷
(自宅)　1910043 東京都日野市平山 3-3-18

Key Words :
BAS, IP, RLG, validation, quantitative WBA

Instruments for Radiation Measurement in Biosciences： Series 3. Radioluminography. 7. Systematization of Radioluminography as a QuantitationTechnique, Detection Characteristics, Validation and a Quantitative Whole Body Autoradiography. Shigeo BABA： Nemoto Life Science Laboratories, Nemoto ＆ Co., Ltd., Mitsukaido-shi, Ibaraki Pref. 300-2521, Japan, （Residence） 3-31-8, Hirayama, Hino-shi, Tokyo 191-0043, Japan.

はじめに

いまや， ラジオルミノグラフィ（RLG）は放射能の二次元分布画像の解析手段としては不動の地位を確立した。 放射能の測定精度は測定時間の平方根に比例して向上する。 したがって， 従来の放射線計数の測定に相当する露光とデータ解析を分離したことによって， 測定時間を桁違いに長くできる RLG では高い測定精度が期待できるはずである。 実際， 72時間露光し， バックグラウンド （BG） の位置依存性を補正して解析した場合の 14C の検出限界は数 mBq にも達している。 しかしながら， RLG は放射能定量測定法としての市民権を得ていないように思われる。 その原因は， 感度と BG 値の面均一性を試験し， 不均一性が認められた場合には補正するという二次元放射能測定法としてのキーポイントが未解決のままであること， また自己吸収， 測定値の統計変動， PSL 値の Bq 値への変換など， 放射能測定法として最も基礎的な事項が放置されたままであることにある。

本稿では， 放射化学の原点に立って RLG の検出特性を考察し， 何をバリデートするべきかを論じ， 感度や BG の位置依存性を補正する方法として測定値のノルマライゼーションという新概念を提案する。 BG の新測定法， IP の汚染検査法， PSL 値の Bq 値への変換法などを提案し， 全身オートラジオグラフィ （WBA） 切片各臓器の厚さを正確に求めて自己吸収を補正し， 非破壊的に WBA 切片上の各臓器の放射能を絶対定量する方法を紹介する。

1.　RLG の検出特性

RLG は， 従来の放射線検出法とは異質なものと考えられ勝ちであるが， 本質的には従来のシンチレーション計数法と同じ原理に基づく検出法である。 両者の差はささいなものである。

従来のシンチレーション計数法では， 放射線による蛍光を放射線粒子ごとに波高選別器で選別し， ある強度以上の信号のみを一つの計数として読み取っているのに対して， RLG では， IP の感光層に到達した放射線のエネルギーを Eu2＋ の励起という形で蓄積し， BAS による解析時にこのエネルギーを PSL に変換し， 画素子ごとに PSL 量の強度に応じていくつかのチャンネルに分けて読み取っている。

初めて RLG に接したとき， ラチチュード， sensitivity， 階調などの用語に惑わされると思われるが， これらはシンチレーション計数装置における検出器の印加電圧， 波高選別器の上限ならびに下限電圧， シンチレーションスペクトロメータにおけるチャンネル数などと読み換えて考えれば当たらずとも遠からずである。 また， 液シンで波高選別電圧以下の信号は拾わないことは， RLG である値以下の PSL 値を 0 と読むことに， 液シンで cpm の Bq （dpm） 変換に唯一しなければならないクエンチングの補正は， PSL の Bq 変換に自己吸収の補正が必要であることに対応している。

1.1.　放射能の算出式

RLG の原理については開発者の解説1），2） があるが， RLG を定量的な観点から扱った論文はない。 まず， RLG の体系化にはいかなる問題があるかを明らかにするために RLG の検出特性を述べる。 ある関心領域 （region of interest, ROI） にABq の放射性同位体 （RI） を含む測定試料を一定時間 IP に露光し， ただちに BAS で解析して得られる PSL 値 （PSLOB） はAと式（ 1 ）で関係づけられる。 PSLBG は BG 値である。 また， 液シンでは壊変率 dpm は計数率 cpm と計数効率 E から式（ 3 ） で算出されている。

k は， 1 Bq の RI から露光時間内に放射された放射線の全エネルギーがIPに入射したと仮定したときの PSL 値 (積分値) で， 感度に相当し， k(24h)のように露光時間を付記する。 f は検出効率 （測定試料から放射された全放射線エネルギーに対して IP に入射する放射線エネルギーの割合） で， 幾何学的効率〔fg，密着露光する WBA 切片や TLC では0.5，RLG 用マイクロプレート （MP）3） ではMPのウェル底面がIPを望む立体角として求められ4)， それは0.13〕， 測定試料と IP の間に存在する物質による吸収 （fab） と自己吸収 （fs,ab） などによって左右されるほか， 32P のような高エネルギー β線やγ線では感光層の透過による損失も係わってくる。 しかしながら， 1 枚の IP で同時に露光された一連の試料においては， これらのうち変動するのは fs,ab だけである。

k は， IP が放射線のエネルギーを吸収する効率 （IP の応答感度， kIP） と， この吸収されたエネルギーを BAS が PSL として読み取る効率 （PSL 読取り効率， kBAS） の積である。

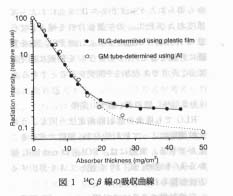
kIP は， IP に入射した放射線により生成する Eu2＋ 励起分子種 （PSL 現象の媒体になる） の個数に相当する。 この値は， a） IP の保護膜や感光層の厚さ， b） この励起反応の G 値， および c） 放射線の線質とエネルギーなどによって決まる。 保護膜の比重を1.4とすると， 保護膜の厚さ （10μm） は 1.4 mgcm2 に相当する。 32Pβ線や BG 放射線に対しては保護膜による吸収を考慮しなくてもよいが， IP に入射した 14Cβ線の約 30％ は保護膜に吸収される （図 1） 。 また， 保護膜の厚さにおける 0.1 mgcm2 の変動が 14Cβ線に対する kIP を約 3 ％変動させることになる。 このことから， 保護膜の厚さの均一性が 14Cβ線感度の均一性に決定的な影響を持っていることがわかる。

kBAS は， 1 個の Eu2＋ 励起分子種が基底状態に戻るときに放射する PSL 値， 読取り過程でレーザー光スキャンによって基底状態に戻る Eu2＋ 励起分子種の割合， BASの解析条件などによって決まる。

上述のように， kIP および kBAS にはあまりにも多くの変動要因があるので k を常数化することはできないし， またその必要もない。 その理由は， 測定試料は普通標準試料と同時に露光されかつ解析されて後者との比較によって放射能を算出する方法が採られているからである。

各 RI についてある条件下における Bq 当たりのおおよその PSL 値を知っていることは測定値の統計変動を考えたり， 測定値を予測する上で意義がある。 無限薄の 14C または 32P を MP のウェルにとり， 乾燥後， ルミラー膜を介して24時間露光し， ただちに解析 （ラチチュード 4， 感度10000， 1024階調） した場合， それぞれ正味で 165 PSLBq3）， 975 PSLBq5） が得られた。 14C ではルミラー膜および空気層による fab を0.7とし， 32P では吸収を無視して計算する。 この場合の 14C および 32P のk（24 h） は約1840， 7500という値になる。 また， ウェル内に存在する 1 Bq の 14C, 32P から IP 表面に到達するβ粒子数は， fg と fab からそれぞれ約7840個， 11200個と見積もられる。 換言すれば 14C, 32Pβ粒子は平均して約 0.021 PSL, 0.087 PSL を与えることになる。

半減期の十分に長い RI を時間を変えて露光し， 同一条件で解析した場合， 数時間までは露光時間に比例して PSLOB は大きくなるが， そのうちこの比例性は成立しなくなる。 これは， Eu2＋ 励起分子種が無放射遷移して基底状態に戻る過程， fading があるからである。 この過程による PSLOB の減少割合は露光時間， 露光から解析までの時間や露光温度なども関係してくる。 単純化するために， 露光温度は一定とし， 露光終了後ただちに解析することにすると fading による損失割合は一定になり， これらの因子は除外できる。

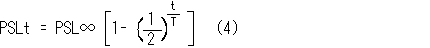fading にはいくつかの経路が存在する6）といわれているが， 単純化するために fading 経路は一つで， その半減期は T として扱う。 露光時間と PSL 値との関係は放射化の式7）と同じように扱うことができる。 いま， t 時間露光後ただちに解析して得られる PSL 値を PSLt， 無限大時間露光した場合のそれを PSL∞ とすると， PSLt は式( 4 )で与えられる。 この式は， fading の 1， 2， 3，...... 半減期相当時間露光した場合には PSLt は PSL∞ の0.50， 0.75， 0.88，...... に達することを意味している。

fading 速度定数と露光温度の間にはアレニウスの式が成立する。 すなわち， 温度が低ければ低いほど fading による損失は少なくなるので， 長時間露光する場合には低温露光が有利である。 しかし， 不注意に低温露光すると結露などによって IP が損なわれる恐れがある。

このほか， IP に蓄積された放射線のエネルギーが散光によるクエンチングによって失われる過程もあるので， 低レベル放射能を扱う場合には暗室での操作が望ましい。

1.2.　市販の標準線源の利用について

市販の標準線源を定量に利用しようとする方法が習慣的に採用されている。 市販の標準線源は BAS 間や IP 間の PSL 値の比較には便利であるが， 放射能絶対測定法としては次の二つの serious な問題があるのでこの方法は推奨できない。 第一の問題は， ここで比較しているのは放射能ではなく両者の表面β粒子束密度であることである。 市販の標準線源と試料の厚さは異なるので fs, ab を補正しない限り， この方法では放射能の比較測定はできない。 第二の問題は double standard になることである。 長さ， 時間， 質量などの基本的な物理量はどの装置を使っても同じ値 （われわれが必要とする精度において） になるが， 絶対放射能の測定ではかなりの誤差を避けることができない。 トレーサ実験の全段階における放射能計測が研究室所有の液シンを基準にしてなされてきたのが最後の段階で標準線源メーカーの標準線源を使うことになる。 したがって， たとえ fs,ab が補正できたとしても double standard の問題が残る。

1.3.　 β線の吸収に関連する事項

前項でも述べたように，β放射体の測定ではβ線の吸収現象が深く係わってくる。 3H から放射されるβ線のエネルギーは極端に小さい。 したがって， 3H の測定には保護膜のない IP が用いられている。 また， 測定試料と IP の間に汚染防止の薄膜を置くことはできないし， fs,ab の補正はできないと考えた方がよい。 14C で代表される軟β放射体 （35S, 45Ca, 33P） では fs, ab の補正が必要である。 それに対して 32P は透過力が大きいので吸収や自己吸収に対する考慮はまったく無用で， むしろ cross talk に対する対策が必要になる。

厚さを mg/cm2 で表したβ線の吸収係数は物質の種類にほとんど依存しないことが知られている。 IP の保護膜や感光層および， IP の RI 汚染防止目的で使うプラスチック薄膜の厚さは例外なく m 単位で表示されているが， RLG の検出特性を論ずる場合にはこの表示は不適切で， 厚さは mg/cm2 で表示しなければならない。

図 1 は， RLG および GM 計数管で作成した 14Cβ線の吸収曲線である8）。 図 1 は放射化学的に二つの興味ある事実を明らかにしている。 その一つは， 吸収係数は測定法によって若干異なることである。 この差は， GM 計数管では波高選別器を通過したβ粒子の個数を数えているのに対して， RLG では IP 感光層に入射しβ線のエネルギーを量っていることによる。 RLG における 14C の fab や fs,ab を論ずる場合には， RLG で求められた吸収係数 （0.30 cm2mg） を使わなければならない。 もう一つは制動放射線の発生率である。 制動放射線の発生率は， 相互作用する物質の原子番号の 2 乗に比例するので， Al を吸収体として求めた GM 計数管の方がより高くなるはずであるが， 実際には逆である。 これは， RLG では制動放射線に対する応答感度が GM 計数管に比べて相対的に高いことに起因していると説明される。

拡大	図１　14Cβ線の吸収曲線

1.4.　放射能の算出における問題点
式（ 2 ） と式（ 3 ） は同形であるが， 両者の間には本質的な差がある。 すなわち， 液シンでは全試料が同じ BG の下に計数処理され， 若干変動する E は自動的に補正されている。 これに対して， RLG では感度および PSLBG は IP 全面にわたって一定であるという前提で処理されている。 問題は， この前提がどこまで成立しているかについての確証がないまま使われていることである。 "RLG では相関係数のきわめて高い検量線が得られるので定量精度も高いはずである"と過信されてきた嫌いがある。 検量線や PSLBG はあくまでもそれを検討した ROI 内での話であって， その値が IP 全面にわたってそのまま通用するとは限らない。 後述するように， 感度および PSLBG には位置依存性がある。 当然のことながら， BG 試料を置く領域 （ROIBG） および標準試料を置く領域 （ROIST） は IP の周辺部に設定することになる。 したがって，最も重要なことは，ROIBGおよびROIST から得られたデータから， IP 全面にわたって感度および PSLBG の位置依存性を補正して任意の ROI の PSLOB－PSLBG(net PSL 値）を精確に評価できる方法，およびkfを精確に補正して Bq 表示できる方法を開発することである。

1.5.　PSL 値の Bq 値への変換

RLG でも従来の放射能測定法と同じように比較測定によって放射能を Bq 単位で求めることができる。 実際には， ROIST の net PSL 値から kf を求め， 式（ 2 ） を使ってAを算出する方法が採られている。

自然科学のあらゆる分野において"物理量はできるだけ SI 単位系で"という趨勢にもかかわらず， RLG では依然として PSL が使い続けられている。 著者は， PSL は放射能の単位になり得ないことを指摘し， 最初から"PSL に代って Bq 表示を使用するべきである"と主張してきた9)。 PSL 値を Bq 値に変換する一般式は存在しない， PSL は次元が異なるので s－1 の次元をもつ Bq へは変換できないという意見10） もあるが， これらは思い違いである。 RLG では全試料が同時に処理されるので露光 （計測） 時間があまり気にされないだけで， もとを質せば s－1 の次元が含まれている。 また両者は式（ 1 ） によって関係づけられる。 計量値 （RLG） と計数値 （液シン） の問題も本質的なものではない。 たとえば， キュリーメータや電離箱式サーベイメータは電離作用 （計量値） に基づいて放射能を測定しているが， 標準試料との比較によって測定値を Bq 単位で表示している。 PSL も標準品との比較によって Bq に変換できる。 このことは， 定量 WBA によっても検証されたことである （3. 参照）。

最近の放射線計数装置はブラックボックスの中で計数率を Bq （または dpm） 変換し， Bq 表示しているので， あたかも絶対測定しているように錯覚し勝ちであるが， 実際にはこの変換には数％の誤差を伴っている。 たとえば， 液シンによる計数効率の外部線源法による補正は，γ線の二つのチャンネルの計数率の比から行っているが， この場合クエンチングの種類， 二つの計数の統計誤差などが誤差要因になっている。 RLG では， 検出特性で述べたように， 1 枚の IP で測定された一連の試料においては検出効率を変化させるのは fs, ab だけであり， はるかに単純で， 直接的にしかも同時に比較測定することになる。 したがって， RLG で求められた Bq 値の精度は， 複雑な計算過程で Bq への変換が行われている一般の放射線計数装置よりも高いと考えて差し支えない。 このことは， RLG と液シンの検量線を比較した図 8 からも頷けることである。 なお， fs,ab の補正法については 25 で述べる。

２　RLG のバリデーション

BAS の開発初期において， 60Coγ線や 14Cβ線を照射した IP を用いて BAS の出力像の定量解析や fading について基礎的な検討が行われた11） が， その後 RLG の定量測定法としての系統的な研究は行われていない。

RLG は TLC12）， WBA13） に応用され， 大きな成果を挙げている。 最近， 薬物動態の研究分野では測定値の信頼性を保証するために測定装置および方法のバリデーションという概念が導入された。 この概念は自然科学のすべての領域にも適用されるべきであると考える。 最近， 20数施設が参加した RLG バリデーション検討分科会は， 各施設が， 14C 平面線源 （順次回送された） を用いて IP および BAS の性能を検討した結果を集計して最終報告書を公表14） した。 そこでは， 「感度の面均一性」 と 「PSL 値の直線性」 をバリデートしているが， その内容はさらに具体化しなければならない。 感度の面均一性は kIPと kBAS に分割して統計的解析を行うべきであるが， 縦横 2 方向でしか検討していない。

RLG のバリデーションには画像の分解能のバリデーションと測定値の精確さのバリデーションの二つがある。 前者には画素子のサイズが問題になるが， 現在最も汎用されている BAS 2000 のそれは 100μm で， これは WBA や TLC に求められる分解能に比べてはるかに小さいので， RLG をマクロオートラジオグラフィとして使っている限り分解能のバリデーションは必要ないと思われる。 最近， "RLG では結果は速く出るが， 画像分解能が悪いので本番は X 線フィルムで"という声をしばしば聞くが， これは思い違いである。 画像分解能が悪いのは， 露光時間が短いので IP に到達する画素子当たりのβ粒子数が少なく， そのため統計変動が大きくなり， その結果画像が粗くなっていることによる。

2.1.　何をバリデートするべきか ？

検出特性の考察から RLG のバリデーションは次の三つの事項に要約されることがわかる。

1.　感度の面均一性試験法を確立する。
2.　PSLBG を正しく評価する。 IP の RI 汚染検査法を確立する。
3.　検出効率， 特に fs,ab を精確に補正し， 測定値を Bq 表示する。

ここで強調すべきことは， 放射能の算出は各 IP ごとに標準試料の値との比較測定によってなされていることである。 個々の IP の kIP や BAS の kBAS に若干の差があっても， これらがある規格値の範囲に入っている限り何の問題もない。 標準 IP や BAS を作って PSL を一つの単位としようとする考え方は無意味である。

2.2.　感度の面均一性試験

前述したように， 感度の面均一性には IP の kIP と BAS の kBAS における均一性が関係している。 実際には両者が重なった状態でしか観察されない。 したがって， この両者が感度の不均一性にどのように係わっているかを明らかにしなければならない。

2.2.1.　147Pm 平面線源

感度の面均一性を試験するには， 均一に放射線照射された IP が必要である。 照射する放射線としては， RLG の測定対象から考えてβ線が望ましい。 IPにβ線を均一に照射するには， ①無限遠の距離にある点線源から照射する （β線の吸収を考えると真空中で）， ②直線状の線源の上を一定速度で IP を移動させる， ③面線源に密着露光する， の三つの方式が考えられる。 これらのうち， 装置の簡単さ， 必要な放射能から実用化できるのは③である。

実用的な露光時間 （たとえば， 10分間） 内に統計変動が問題にならない数のβ粒子を入射させるためには表面β粒子束密度が十分に高い （たとえば， 10000βmm2/min） 平面線源が必要である。 14C は半減期が長いのでβ粒子束密度の高い平面線源を作製できないばかりでなく， 破損した場合の廃棄に難問題が残る。 これに対して， 147Pm（2.26 y, 0.224 MeV, 微弱な 0.121 MeVγ ） ではβ粒子束密度の十分に高い平面線源を作製でき， 破損しても decay out を待って廃棄できるという利点がある。 以上のような理論的考察に基づいて， 147Pm 平面線源を用いて感度面均一性を試験する方法を発表した （第11回 RLG 研究会， 平成 8 年 5 月）。 ここで用いた 147Pm 平面線源は， WBA 切片の臓器厚さの測定15）に作製したものである。 なお， この線源の作製時における 147Pm の密度は約 0.5 MBqcm2 で， 147Pm 層は無限厚さである。 その後， Ray Test 社から同じ目的に使われる 14C 平面線源が提供されたが， その表面β粒子束密度は著者らの平面線源の15分の 1 で， そのために長時間の露光が必要である。

2.2.2.　試験法と統計解析

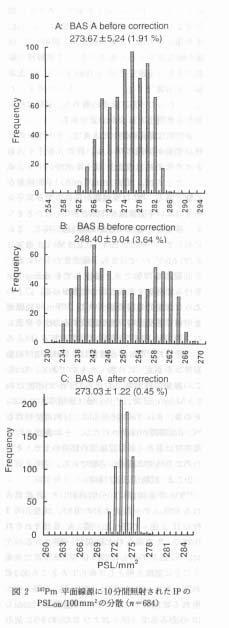
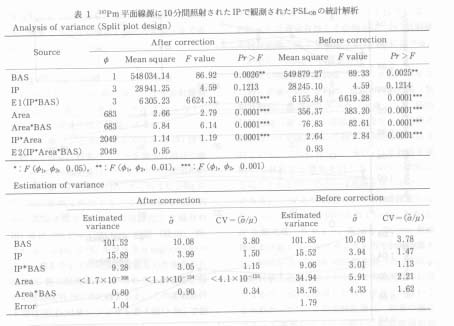
147Pm 平面線源に10分間照射した IP に見られる PSLOB の分散を 2 台の BAS， 未使用の 4 枚の IP を使って調べた。 図 2 A, B はそれぞれ BAS A, B で得られた結果の一例である。 次に， 147Pm に照射した別の IP を BAS A で画素子ごとに感度を補正して解析したところ図 2 C が得られた。 この場合， PSLOB に不均一性が現れる要因として， 147Pm 平面線源 （area）， IP の応答感度 （IP） および BAS の PSL 読取り機構 （BAS） の三つがあり， これらが独立に PSLOB に不均一性を引き起こすことになる。 重要なことは， これらの変動要因が PSLOB の不均一性にどのような貢献をしているかを統計的手法で解析することである。 そこで， 得られた計測結果を分割法で解析した。 ただし， 解析は計算の便宜上周辺部 10 mm を除外した 10×10 mm の684エリアの PSLmm2 を検討することにより行った。 解析結果を表 1 に示した。

表 1 から明らかなように， この不均一性の主因は BAS の読取機構にあり， 次いで IP であった。 また，PSLmm2 の SD は 147Pm 平面線源を用いる補正によって劇的に縮小し， 本法の有用性を検証できた。 したがって， この補正は BAS および IP ごとに実施する必要がある。

2.2.3.　測定値のノルマライゼーション

感度や PSLBG にある程度の位置依存性が現れることは避けられないことである。 著者はこれを補正する有効な方法として測定値のノルマライゼーションという新概念を提案する。 図 2 C は， BAS A について画素子ごとに PSL 読取効率を補正し， 各エリアの PSLOB を平均値にノルマライズして得られた PSLnor.mm2 の分散である。 補正前に1.91％あった RSD が顕著 （0.45％） に向上しているのがわかる。 したがって， PSLOB の代りに PSLnor. を使えば測定精度は著しく向上するはずである。

2.2.4.　感度に見られる方向性

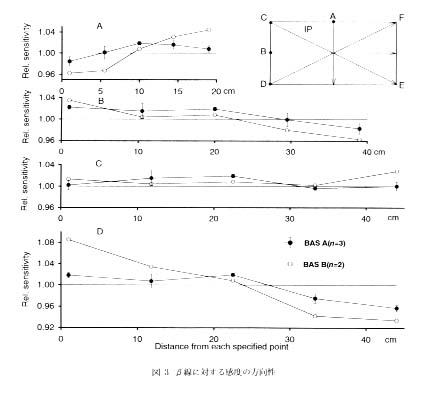
感度の不均一性の実体を調べるために， 147Pm 平面線源に照射した IP について縦横の中心線および 2 本の対角線上に沿って等間隔にいずれも 5 個の， 合計17エリアの PSLmm2 を調べ， 全エリアの PSLmm2 の平均値に対する比， relative sensitivity を検討した。 このように指定した17エリアを使えば， 合計 4 方向の relative sensitivity の変動が検討できて便利である。 BAS A については 1 か月間隔で 3 回実験を行った。 実験結果を図 3 にまとめた。 これより重要な三つの結論が得られた。

その第一は， relative sensitivity は比較的再現性のあることである。 このことは， あらかじめ 147Pm 平面線源を使って所有の BAS を校正しておけば感度の位置依存性は補正できることを示唆している。 後述する PSLBG の諸データは BAS A で得られたものであるが， PSLBG の位置依存性の現れ方（図 4 および図 5 ）は図 3 で示した BAS A の結果とよく一致している。

その第二は， relative sensitivity の検討は単に中心線に沿って縦・横 2 方向だけの検討では不十分であり， 対角線方向も調べなければならないことを意味している。 特に興味深いことは， 左上から右下への変動とは対照的に左下から右上にかけて大きな変動が見られることである。 これは， BAS 解析時におけるレーザー光スキャン軸が微妙にずれているためによるものではないかと考えている。

第三は， ROIST で作製した検量線をそのまま適用することの危険性である。 たとえば， BAS B で D 付近で作製した検量線をその対極 （すなわち， F） に適用すると， D を1.00とした場合0.85と低く， 誤って見積もってしまうことである。

2.2.5.　BAS の感度面均一性試験

BAS A, B で認められた感度の方向性がどれだけ普遍性があるか， また現在稼働している BAS のβ線感度の面均一性がどのくらいであるかなどは不明であるが， BAS Bに見られるような大きな不均一性があることに気づかずに使っている可能性も否定できない。 他方， 感度の位置依存性は比較的経日変化の少ないことが明らかにされた。 したがって， BAS の感度の面均一性試験を定期的にまたは感度の面均一性が疑われた時点で実施し， ① PSLOB の RSD が， たとえば 2 ％ 以上の場合には再調整を行う， ② 684エリアの PSLOB および PSLnor. の分散 （図 2） および感度の各方向にわたる変動 （図 3） を記録しておくことにしたら， RLG の信頼性は一段と高められると考える。

ここで指摘しておきたいことは， 感度の面均一性試験に必要なのは， 147Pm 平面線源ではなく， この平面線源に照射された IP （147Pm irradiated IP） であることである。 宅配便で， カセットに納めて供給された 147Pm irradiated IP を使うことによってどの施設でも所有の BAS の面均一性を試験することができる。 147Pm irradiated IP の輸送について懸念されるかも知れないが， まったく問題ない。 147Pm irradiated IP は， 放射能分布情報を記録したもの （すなわち， 現像前の X 線フィルムと等価） であって， 放射能ではない。 また， 147Pm irradiated IP の PSL 密度は 300 PSLmm2 前後である。 輸送時にカセット内の IP が受ける BG 放射線 （2 PSLmm224 h 前後） や fading の影響は均一である。 このような理由から， 輸送はこの試験に対してなんらの障害にもならない。 実際， 図 2 B は， 宅配便で送られた 147Pm irradiated IP を使って得られた結果である。

厳密な面均一性試験を定期的に行うとしても， 面均一性がある時点で損なわれ， それに気付かずに使用していて次の定期試験まで誤った測定値を出し続けている恐れもある。 より簡便な面均一性試験として， 前述した17エリアの中心点に一定量の 14C または 147Pm をスポットして作製した簡易線源に露光し， 解析して感度の各方向にわたる変動 （図 3） をモニタする方法を提案する。 この方法は簡便ではあるが， 全体にわたる均一性についての情報 （図 2 A, B） を与えない， また画素子単位での感度の補正ができない （図 2 Cは得られない） のであくまでも先に提案した方法の補助手段と考えるべきである。

2.3.　PSLBG の問題

RLG における BG 値には， 二次元放射線検出法として新しく考えなければならない， PSLBG の位置依存性の問題がある。

まず， 液シンとRLGのおおよその BG 値を比較してみる。 標準バイアルを使った場合の液シンの BG 計数率値(以下， すべて14C測定用ウイドウの値)は大体 30 cpm でこれは 0.5 Bq の 14C の計数率に相当する。 これに対して， 20 mm 真鍮遮蔽で IP を72時間露光した場合の BG 値は 300 PSL100 mm2 前後 （後出） で， これは 0.3 Bq の 14C を厚さ 0.5 mgcm2 のルミラー膜を介して同時間密着露光した場合の正味 PSL 値に相当する。 すなわち， 両者を正味の応答感度対 BG で比較すると， この遮蔽条件下では RLG は液シンよりも若干低い BG で測定していることになる。

式（ 2 ） から明らかなように， RLG において定量精度を支配するのは PSLBG の変動の大きさである。 実際， PSLBG は IP 全面にわたって均一であるか， またどのくらいの変動があるかについてはまったく明らかにされていない。

PSLBG の変動要因として，

a.　感度の面均一性
b.　BG 放射線の統計変動
c.　遮蔽むら
d.　IP の劣化

の四つが挙げられる。 これらのうち， a. は前項で解説した。 b. は遮蔽の強化によって小さくはできても避けることができない要因である。 また， d. は未使用またはよく管理 （後述） された IP を使うことによって回避できる変動である。 結論は， よく管理された IP を使用し， 遮蔽を強化して BG 放射線の統計変動を小さくするとともに感度および遮蔽むらに起因する変動を可能な限り小さくすることである。 以下に， いままでまったく検討されていない PSLBG の位置依存性とその補正法， BG 放射線の統計変動， IP の管理法などについて述べる。

2.3.1.　PSLBG の位置依存性

従来の放射線計数装置では BG を低下させるために遮蔽の強化を初め， 反同時計数回路 （気相計数管， 低バックグラウンド液シン）， 同時計数回路 （液シン）， 波高選別器など， 目的の放射線だけを選択的に計数する機能が組み込まれている。 これに対して， RLG は放射線を選別して検出する機能を持たないので， PSLBG を低下させる唯一の方法は遮蔽を厚くすることである。 このような理由から IP の露光にはシールドボックスが用いられている。 著者は， IP を無遮蔽， カセット， 5， 10， 20 mm 真鍮箱および富士シールドボックス内で24時間露光し， PSLBG5×5 mm の分散を調べた。 PSLBG の絶対値は遮蔽の厚さに対して指数関数的に低くなるが， SD は期待したほど改善されないことがわかった8）。 この実験結果は， 遮蔽の強化によって遮蔽むらという新しい変動要因が加わったこと， したがってこれに起因する不均一性を補正しない限り， 遮蔽効果を完全には活かせないことがわかった。

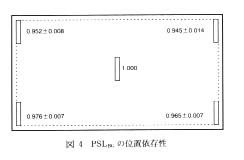
まず， PSLBG の位置依存性を明らかにするために 5 枚の未使用 IP を 20mm 真鍮箱の中で72時間放置し， 四隅と中心部の PSLBG を調べた結果， 図 4 が得られた。 この検討によって， 中心部の PSLBG を 1 とした四隅の PSLBG の比は 1 より小さいこと， しかもこの比には比較的再現性があることがわかった。 前者は， IP の四隅は more thickly shielded andor less sensitive であること， 後者は露光容器内に置かれた IP に見られる PSLBG の分布はほぼ同じであることを示唆している。 ところで， IP の四隅は同じ程度に遮蔽されているが， PSLBG の相対値にこのような差が出たことは感度の位置依存性に起因していると考えられる。 実際に， 図 4 の値を， 図 3 で示した対応した位置 （IP の CDEF 点） の相対感度で補正すると四隅の PSLBG はほぼ同じになる。

2.3.2.　PSLBG の新測定法

図 4 は ROIBG の設定法に対して重大な警告を発している。 ROIBG の設定位置によっては PSL 値がマイナスになり， PSLBG の最も低いところに ROIBG を設定し直してつじつまを合わせているのが実状である。 IP の片隅に設定した ROIBG の PSLBG を固定値として使う方法は一方的に偏った net PSL 値を与えている恐れがある。 著者らは， より合理的な PSLBG の測定法として重ね合わせ法 （superimpose method） を提案した8）。

数枚の IP を重ねて測定試料 （14C） に露光した場合を考える。 測定試料に接している IP を測定用 IP （IPME）， 他の IP を BG 補正用 IP （IPBG） とする。 特殊な場合を除き， 露光操作は実験室内でしかも何らかの遮蔽をした状態で行われている。 この場合， IP の感光層に入射した BG 放射線の透過力は IP の厚さ （100 mgcm2） に対して十分大きいので BG 放射線は IPME および IPBG に対して等価であると考えられ， このことは図 4 のデータからも裏付けられている。 他方， 14C から放射される β線の最大飛程 （約 25 mg/cm2） は IP の厚さに対して十分小さいので測定試料中に存在する 14C は IPBG にはほとんど影響を及ぼさないと考えて差し支えない。 唯一の懸念は， 14C β線から発生する制動放射線であるが， 制動放射線発生率は0.3％以下で， 実際上は問題にならないことが証明された （図 1）。 したがって， IPME のある ROI の PSLBG を， IPBG で得られた当該 ROI の PSLBG から式（ 5 ） で求めることができる。 この場合， IP の感度は一枚ごとに少しずつ異なるが， この差異は同一領域に設定した ROIBG の PSLBG から補正できるはずである。 ここに提案した重ね合わせ法は， 反同時計数回路を用いた低バックグラウンド計数装置と一脈通ずるところがある。

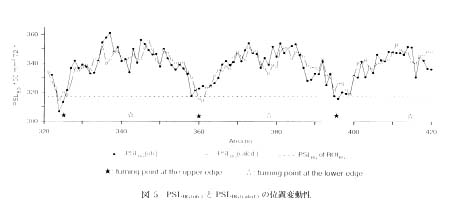
提案した方法の測定精度を試験するために次の実験を行った。 5 枚の未使用 IP を重ねて， 厚さ 20 mm の真鍮箱の中で72時間露光し， 解析した。 最も下の IP を IPME， 他を IPBG とした。 周辺 10 mm をカットし， 18（縦）×38（横） エリアに分画した。 左上端をエリア 1 とし， 下へ 2， 3， 4，......， 17， 18， 折り返して19， 20，......と番号をつけた。 エリア 1 5 および 680 - 684を ROIBG とし， 両 ROI の平均値を PSLBG として用いた。 エリア321から420について PSLBG の実測値 （PSLBG（ob.）） と重ね合わせ法で算出された PSLBG （PSLBG（calcd.）） を比較し， その結果を図 5 に示した。 なお， IPBG の枚数としては 3 枚で十分であることがわかった。

この図において次の 3 点を強調しておきたい。 その第一は， PSLBG（ob.） に明確な周期性が認められることである。 それは， エリア 36 n （n はゼロまたは正の整数） と 36 n＋1 に"深い谷"と 36 n＋18 と 36 n＋19 に"サドル"部分が現れるという周期性である。 エリア 36 n と 36 n＋1 は上辺部の折返し点に， 36 n＋18 と 36 n＋19 は下辺部の折返し点に相当する。 これらの点に相当するエリアを中心に PSLBG が極小値になるのは， これらのエリア付近が more thickly shielded andor less sensitive であることによると思われる。 この場合にも感度の位置依存性が係わっている。 上辺部が"深い谷"に， 下辺部が"サドル"になるのは図 3 A に示した上下方向の感度の位置依存性と一致している。 なお， この周期性は PSL 読取り方向によっても若干異なる。 逆方向に読み取ると， "深い谷"と"サドル"は同じ深さの"谷"になる。

その第二は， PSLBG（ob.） はエリア番号に従って大きく変動するが， PSLBG（calcd.） はこの変動を忠実にフォローしている， 換言すれば提案された方法は PSLBG の位置依存性を精確に補正していることである。

その第三は， ROIBG の PSLBG を固定値 （図中点線） として使用する従来法では PSLBG を 1 エリア当たり平均して約 20 PSL も実際よりも低く （net PSL 値はそれだけ高く） 見積もることになるが， 本法は偏りのない測定値を与える。 また， 684全エリアについて計算すると PSLBG（ob.） と PSLBG（calcd.） の差の絶対値の平均は 5 PSL に過ぎなかった。 なお， 両者の差はゼロにはならない。 これは， PSLBG（calcd.） をいかに正確に評価しても 1 枚の IPME で求められた PSLBG（ob.） は次項で述べる統計変動を伴っているからである。

われわれの興味は， 図 5 に見られる約 50 PSL の変動や 5 PSL の差が 14C ではどのくらいに相当するかということである。 14C をルミラー膜を介して同じ72時間密着露光するとおおよそ 1 000 PSLBq が得られる。 それゆえ， これらの変動幅や差はそれぞれ 50 mBq および 5 mBq 14C に相当するということである。

32P から放射されるβ線のエネルギーは高いので， 32P に対しては重ね合わせ法は適用できない。 この核種に対しては， あらかじめ数枚の IP を使って次項で述べる BG area ratio を求めておき， これで各エリアの PSLBG を推定する方法が有効である。

拡大	図 2　147Pm 平面線源に10分間照射されたIPのPSLOB/100mm2の分散 (n＝684)

拡大	図 3　β線に対する感度の方向性

拡大	図 4　PSLBG の位置依存性

拡大	図 5　PSLBG(ob.) と PSLBG(calcd.) の位置変動性

拡大	表 1　147Pm平面線源に10分間照射されたIPで観測されたPSLOBの統計解析

2.3.3.　BG 放射線の統計変動

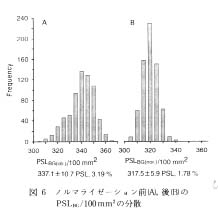
従来の放射線測定法では測定値に SD をつけて提示するのが基本中の基本になっている。 PSLBG がどのくらいの SD で測定されているかについてはまったく明らかにされていないが， BG area ratio による補正によって PSLBG の統計変動を論ずることができる。 BG area ratio とは ROIBG と各 ROI の PSLBG の比である。 IPME および IPBG における PSLBG の分布は同じであるので， 両 IP における各 ROI の BG area ratio も同じになると考えられる。 したがって， 各エリアの PSLBG（ob.）をBG area ratio で割る(式（ 6 ）)ことは， 各エリアの PSLBG（ob.）を ROIBGのPSLBGにノルマライズすることになり， かくして得られた値（PSLBG（nor.））は， BAS の kBAS および遮蔽むらに由来する位置依存性を補正した値になる。 図 6 A, B はそれぞれ PSLBG（ob.）, PSLBG（nor.） の分散を示す。

　　　　BG area ratio = ratio of PSLBG of an area to that of ROIBG in IPBG

PSLBG（ob.） とは対照的に， PSLBG（nor.） は典型的な正規分散になっていることに注目されたい。 これは， 後者では kBAS や遮蔽むらによる不均一性が完全に補正され， BG 固有の統計変動を示していることを意味している。

液シンで得られる計数率は放射性壊変率と計数効率によって関係づけられ， 計数値として普通 n±√n で与えられる。 これに対して， PSL 値も離散分布の統計量として扱うことができる。 次に， 図 6 B に見られる統計変動を身近なβ放射体の壊変に換算してみよう。

PSLBG（nor.）100 mm2 が317.5±5.9（RSD： 1.78％）(図 6 B) の 317.5 PSL は， 前述した32Pβ粒子 1 個当たりの平均 PSL 値から3 650個の 32Pβ粒子が入射したときに予想される値に相当し， その放射性壊変に伴う統計変動の RSD は （√3650/3650　ｘ　100＝）1.66％で， これは PSLBG（nor.） の RSD とほぼ一致している。 他方， 同じ計算を 14Cβ粒子について計算すると， RSD は0.81％になり， PSLBG（nor.） の RSD よりずっと小さい値になる。 これは次のように説明される。 先述したように BG 放射線は IP を完全に透過していると考えられる。 14C β粒子はIP の保護膜に約30％吸収され， 感光層の表層部で完全に吸収されてしまうが， 32Pβ粒子の大部分は感光層を透過している。 したがって， BG 放射線の統計変動を論ずるモデル放射線としては 32Pβ線がより適している。

もう一つ指摘したいことは， PSLBG（nor.） の測定精度である。 液シンの BG 計数率は 30 cpm 前後である（32±√32ｘ100/100　＝　32±0.6）。

PSLBG（nor.） は， 液シンに置き換えると BG 計数率を32±0.6cpmで測定していることに相当しこれだけの精度を確保するためには100分計測が要求される。

このことは， いかに RLG が低レベル放射能の測定に有利であるかを示唆している。

最後に， ROIBG の設定についても私見を述べる。 普通， かなり広い面積を ROIBG に指定し， PSLBGmm2 の平均値を PSLBG として使っている2）。 しかし， 検出限界は BG 値の変動を基準にして定義されるので， この方法では検出限界を論じられない。 数個の， 測定対象とほぼ同じ面積 （25 - 100mm2） の ROIBG を設定し， その PSLBG±SD を表示するべきである。

拡大	図 6　ノルマライゼーション前，後の PSLBG100mm2の分散

2.3.4.　IP の劣化

IP を反復使用できることが， RLG の利点として挙げられているが， この利点は， IP が劣化していることに気づかずに使用して， IP が誤った値を与え続けている危険性と裏腹なものである。 IP の耐久性について， メーカー側から"1000回使用しても問題ない"とか， "少し黄変するが問題ない"という曖昧な説明10) がなされているが， もっと厳格な試験が必要である。 IP の劣化には次のタイプがある。

a.　IP 全面にわたってkIPがほぼ均一に低下してゆく。
b.　RI 汚染によって， 局所的に falsely high net PSL を与える。
c.　IP 保護膜の剥離 （14Cβ線に対しては， 保護膜による吸収損失がなくなるので， kIP は約 30％ 大きくなるが， 32Pβ線や BG 放射線に対するkIPは変らないはずである），結露による応答感度の低下などである。 以下， このタイプの劣化を IP の損傷という。

これらのうち， タイプ a. の劣化は感光材料の経日劣化に起因するものであるが， 特に著しい劣化でなければ問題はない。 また， このタイプの劣化は"このIP は他の IP に比べて全般的に低値を与える"という感触から研究者も気づく劣化である。 これに対して， RI 汚染と IP の損傷による劣化は気づかれ難く， しかも測定値に大きな影響を及ぼす可能性があるのでより致命的である。

2.3.5.　IP の RI 汚染検査法

普通， 露光はルミラー膜を介して行われているが， 何らかの事故で IP が汚染され， 汚染されていることに気づかずに使用し， 汚染箇所が falsely high net PSL value を与え続けている危険性がある。 したがって， バリデーションの立場からは IP の RI 汚染状況を常時モニタすること， および疑わしいデータが出た場合には使用した IP の RI 汚染情報を遡って引き出せるようにしておくことが肝要である。

最も簡単な汚染検査法は， 使用に先立って PSLBG（ob.） の分散を調べる方法であるが， 前述したように PSLBG（ob.） には位置依存性があるので精確な試験結果は得られない。 そこで， より理論的でしかも実用的な IP の RI 汚染管理法を提案する。 その骨子は， 汚染検査をする IP （IPEX） と複数枚 （3 枚が実用的） の BG 補正用 IP （IPBG） を重ねて露光し， IPEX の各 5×5 mm エリアの PSLBG（nor.） を求め， これを指標にして汚染を検討することである。

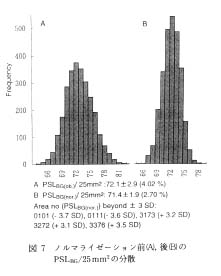
図 7 は実験結果の一例で， 72時間， 20 mm 真鍮箱の中で露光した場合の PSLBG（ob.）25 mm2 と PSLBG（nor.）25mm2 の分散を示す。 この場合にも， PSLBG（nor.）25mm2 は典型的な正規分散になっている。

RI 汚染の判定基準としては，

1.　PSLBG（nor.） が 4 SD を超えるエリアがある IP は汚染 IP と判定し， 使用しない。
2.　3 SD を超え， 4 SD 未満のエリアは擬汚染エリアとし， 以降監視を続ける。
が妥当と考える。

なお， 汚染の検討の単位として 5×5mm を採用したのは， この面積があまり広いと点汚染が希釈されてしまうこと， またあまり狭いと汚染の位置決めが困難になるからである。 このサイズにすれば， IP の全エリアを 4 桁の数で示すことができる。 すなわち， 前の 2 桁 （01～36） は測定領域上辺からの距離， 後の 2 桁 （01～76） は左辺からの距離を示す。 たとえば， この実験例で擬汚染エリアの一つ， 3173は上辺および左辺からそれぞれ 31×5 mm， 73×5 mm の位置にあるエリアを示す。 このように番地をつけておけば， 解析時に IP の位置が若干ずれても汚染箇所の位置決めが容易に行える。

われわれの最大関心事は， この方法でどのくらいの 14C 汚染 （Bq25 mm2） が検出できるかということである。 前記の露光条件(72時間)で 125 mBq の 14C をルミラー膜を介して露光した場合 140 PSL を与える （後出， 図 8 C）。 ルミラー膜による吸収を考慮すると， 100 mBq の汚染が 132 PSL を与えることになる。 したがって， この判定基準を適用した場合には 6mBq 14C25 mm2 以上の汚染が検出されることになる。 露光条件が変われば当然検出限界も変わる。 カセット内で24および72時間露光した場合の検出限界はそれぞれ22および 12mBq 14C25 mm2 であった。

拡大	図 7　ノルマライゼーション前，後のPSLBG/25mm2の分散 RLG 試料 ： fg＝0.50， fab＝0.85， fs,ab＝1.00

2.3.6.　IP の損傷試験

IP の損傷は， 損傷部位の PSLBG（nor.） の変動となっても現れるはずである。 しかしながら， BG 放射線自体にかなり大きな固有の統計変動があるので， "PSLBG（nor.）の 4 SD"を損傷の判定基準とすると約10％の感度の変動がないと損傷と判定できない。 これでは損傷試験としては甘すぎるように思われる。 IP の損傷試験としては 147Pm 平面線源に露光した IP を感度校正した BAS で解析し， PSLnor. の分散を検討するのが妥当である。 PSLnor. の RSD は0.5％である （図 2 C） のでこの方法によって応答感度 2％ 前後の損傷が検出できる。

2.3.7.　IP の管理法

IP の汚染 （損傷） 管理の難しさは， 汚染の日時や程度が特定できないままに徐々に進行して行くケースが多いと考えられることである。 同じようなことはすでに普通の放射線計数装置でも経験済みである。 著者はラジオ TLC スキャナーを次のように管理していた。 測定ごとに余分に 1 分間ずつスキャンニングさせ， その結果に測定者と日付を記入させてファイルさせた。 こうすることによって， 強度の汚染は BG の突然の上昇によって， また， 軽微な汚染でも繰り返されるとはっきり判定できた。

バリデーションの一環として， 次のような IP の管理法を提案する。 各研究室の IP について IP の識別番号， 試験日， PSLBG（ob.） と PSLBG（nor.） の分散図および PSLBG（nor.） で ±3 SD を超えたエリアの番号とその値をマイコンに記録し， 必要な場合はいつでも読み出せるようにしておく。 汚染による擬陽性エリアは反復して現れることによって特定できるはずである。 このような IP は"汚染管理された IP"であり， これによって得られるデータの信頼性は一段と高まるものと考えられる。 1 回または 1 枚の IP のデータから結論は得られないが， 反復して PSLBG（ob.） と PSLBG（nor.） の分散図をフォローしておれば感度や BG の位置依存性について次第に明白な傾向がつかめるかも知れない。 このことは， 1 枚の IP による検討からは何も見えなかったが， 5 枚の IP のデータを検討することによって PSLBG の位置依存性 （図 4） が浮かび上がってきたことからも言えることである。

2.4.　低レベル放射能の検量線

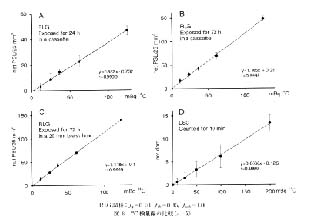
従来の放射線測定法での経験が教えるように， 低レベル放射能の測定精度は BG 値の変動をいかに低下させるかにかかっている。 PSLBG の変動要因としては， 感度と遮蔽むらによる不均一性， IP の RI 汚染および BG 放射線の統計変動の三つが考えられる。 これらのうち， 第一の要因は重ね合わせ法によって補正できる。 第二の要因は"管理された IP"を使用することによって避けられる。 最後の要因は遮蔽の強化によって低下させることはできても 0 にすることはできない要因である。 図 8 は， 図中に示した三つの条件下で露光して作製された 14C の検量線と， 比較のために液シンで作製した検量線である。 いずれの検量線も直線性は優れている。 露光時間と測定値の再現性は A と B を， 露光時の遮蔽厚さと測定値の再現性は B と C を比較することにより明らかになる。 なお， 重ね合わせ法では， どこに ROIBG を設定しても原点のごく近傍を通過する検量線が得られることを強調しておく。

現在， RLG における検出限界の値は研究者個人の主観に委ねられているが， もっと客観的な検出限界を定義するべきである。 いま， 放射線計数装置と同じように， 検出限界を， BG 値の 3 SD を超える net PSL 値を与える放射能と定義 （これはいくぶん厳しい基準であるが） する。 露光条件 A, B, C における検出限界をそれぞれの PSLBG の 3SD と検量線の勾配 （PSLBq） から算出するとそれらは約 17， 9， 4 mBq 14C25 mm2 となる。 当然のことながら， 遮蔽が厚いほど， また露光時間が長いほど検出限界は高くなっている。 ROI 面積が広くなれば， 単位面積当たりで示した検出限界は高くなる。 たとえば， 露光条件 C における 100mm2 当たりの検出限界は 13mBq 14C である （図 6）。 図 8 は， RLG は液シンに比べていかに感度が高いかを明確に示している。

2.5.　自己吸収の補正と Bq 表示

RLG では一般に標準試料と測定試料を並べて IP に同時に露光し， 解析している。 先述したように検出効率を左右するのは fs,ab だけである。 したがって， これを正しく補正すれば， 測定値を Bq 表示できる。

自己吸収の度合いは測定する核種によって異なる。 32P の測定では自己吸収の補正は不要であるが， 14C で代表される軟β放射体は自己吸収を強く受けるのでその測定では自己吸収に対する補正は不可欠である。 さらにエネルギーの低い 3H では自己吸収の補正は実際上不可能である。 自己吸収は式（ 7 ） によって補正できる。 この式において， PSL および PSL0 はそれぞれ厚さ dおよび0mgcm2 の試料の PSL 値である。μは RLG で求められた吸収係数で 14C 線のそれは 0.30 cm2mg である。 試料の厚さが半価層の 6 倍以上になる （14Cβ線では 15 mgcm2 以上） と式（ 8 ） で近似できるようになる。

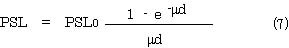
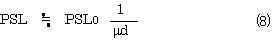
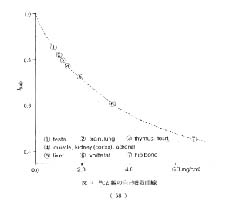
自己吸収は自己吸収補正曲線によっても補正できる。 図 9 は， 一定量の 14C をスポットし， 乾燥した tissue paper を重ね合わせて露光し， 得られた画像 （図11 C） から作製した 14C の自己吸収補正曲線である。 図中には参考までに， 60 m で作製したラット WBA 切片の主要臓器の厚さがプロットされている。 臓器の種類によって fs,ab は大きく異なることを認識しておくべきである。 tissue paper では心許ないと思われるかも知れないが， その厚さは 1.4 mgcm2 前後で， WBA 切片上の各臓器の厚さとほぼ同じであるので， tissue paper は定量 WBA における検量線や自己吸収補正曲線の作製には最も理想的な支持体である。 14C の吸収係数を式（ 7 ） に代入して作製した理論曲線は図 9 の曲線と完全にオバーラップする。

2.5.1.　液状生体試料

薬物の血中濃度の経時変化を調べる方法として， プラズマをポリエチレンを裏張りしたろ紙にスポットし， RLG で測定する方法が三共の中島氏らにより開発された。 著者らは MP を使って液状生体試料を測定する方法を提案している。 両者のメリット， デメリットをプラズマを例にして考えてみる。 なお， プラズマ 1 ml は 60 mg 前後の固形物を含んでいる。 また， ろ紙の厚さは 8 mgcm2 とする。

スポット法の利点は， 操作が簡単であることと幾何学的効率 （fg） が高いことである。 欠点は， 試料自体に起因する自己吸収のほかにろ紙による自己吸収を強く受けることと， スポットの広がりの差が自己吸収に差を与えるのではと懸念されることである。 プラズマ 20μl をろ紙にスポットし， 0.5と 1.0 cm2 のスポットが得られたとしよう。 乾燥した場合， 前者の厚さは 9.2mgcm2， 後者のそれは 8.6 mgcm2 になる。 これらの厚さの自己吸収を式（ 7 ） で計算するとそれぞれ0.31， 0.34になる。 実際には熟練によりスポット面積の広がりはもっと一定にできるので， 本法によるスポット面積の差はあまり大きな誤差を与えないことがわかる。 この場合の fg・fs,ab は0.16， 0.17になる。 MP では底面積は固定 （1 cm2） しているので自己吸収は常に一定になる。 20μl をとったときの試料のfs,ab は図 9 から約0.81と見積もられる。 MP の fg は0.13であるので fg・fs,ab は0.11となり， ろ紙にスポットする方法に比べて検出効率は若干低くなることは避けられない。 しかし， 測定可能な試料量は 0.2 ml である。 すなわち， ろ紙にスポットする方法は少量の液状試料に対してより有効である。 他方， MP は試料液量の大きい試料， たとえば大型動物のプラズマや HPLC 溶離液の測定などに適していると考えられる。

著者らは， 蒸発残留物量がまちまちの液体試料を MP で測定する方法として， 内部標準法を提案する。 その方法の骨子は次のとおりである。

測定試料 （a,b,c,...） を MP の第 1 行のウェル （C-1a,b,c,...） と第 2 行のウェル （C-2 a,b,c,...） に同量ずつとる。 後者には， 放射能既知の， 高比放射能 （すなわち， 自己吸収が無視できる） 内部標準 aBq を添加する。 放置乾燥した後， 常法により RLG を行う。 C-1， C-2 の PSL 値をそれぞれ PSLC-1， PSLC-2 とする。 試料中の放射能 （xBq） は式（ 9 ） から算出される。

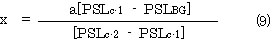内部標準法は， 従来法 （外部標準法ともいうべきである） に比べて操作が若干煩雑であるが， 測定試料そのものの自己吸収を自動的に補正しているので高精度の測定が期待できる。 たとえば， この方法で 0.1 ml のラットプラズマを試料とした場合， 48時間露光で 50 mBq 14C まで定量できた （第13回 RLG 研究会）。 fg のさらに高い MP の試作・使用， 露光時間の延長， 提案した PSLBG 評価法の採用などによって定量限界はさらに向上できると期待している。

2.5.2.　薄層クロマトプレート

TLC 上の低レベル放射能は， 以前には掻き取って液シンで測定されていたが， RLG の登場によって直接 RLG で測定されるようになった。 この場合， 自己吸収が問題になるが， TLC 吸着材層の厚さは， 手製の TLC プレートは別としてきわめて高い精度で品質管理されているので一定と考えてよく， しかも， 14Cβ線に対して無限厚さであるので， 自己吸収は同じプレートにスポットした標準試料のそれと同じであるとして扱って差し支えない。

2.5.3.　WBA切片

WBA 切片の各臓器の自己吸収の補正については次節で解説する。

2.6.　測定値の統計変動

従来の放射線計数装置で得られた測定値は測定試料も BG もともに n±n12 で処理し， 両者を対等に合算して測定試料中の RI の壊変率を求めている。 これらの装置では， 測定試料中の RI も BG も計数としては等価であるのでこのような処理ができる。 これに対して， RI と BG の 1 放射線粒子当たりの PSL 値は異なっているので， RLG では両者を対等に処理して， 測定試料中に存在する RI の壊変数の統計変動を論ずるのは無理がある。

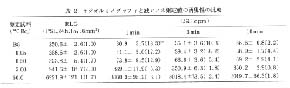
測定試料の PSL 値から， 測定試料中の RI の壊変数の統計変動をどのように論ずるかは今後の検討課題であるが， 著者が行った初期のデータから実用的な結論が得られている。 表 2 は， 0.00 0.05 0.50 5.0 50.0Bq 14C を MP のウェルにとり， 乾燥後 RLG （5mm の真鍮箱内で， 24時間露光） を行った結果と， 液シンで計数時間を変えて測定した結果を比較した表である9)。 なお， 使用した BAS の感度の面均一性は， RSD で1.9％であることが 147Pm 平面線源によって確認されている。 また， これは初期のデータで感度や PSLBG の位置依存性は補正されていない。

液シンの計数結果は教科書的である。 すなわち， 計数時間が長くなればなるほど SD は小さくなる。 また， 計数時間が同じなら放射能が多くなるほど RSD は小さくなっていくが， 0 に近づくかというとそうではなく， だいたい 1 - 2 ％になる。 これは放射能の統計変動のほかに機械的な誤差が前面に出てくるからである。 RLG では， 放射能の多少にかかわらず RSD はほぼ一定で 1 - 2 ％である。 この結果は， 24の結論を裏付けるものである。

拡大	図 8　14C 検量線の比較 (n＝5)

拡大	表 2　ラジオルミノグラフィと液シンの測定値の再現性の比較

３.　定量全身オートラジオグラフィ

Ullberg 以来， WBA は薬物の体内分布の解明に不可欠な技術として使用されてきた。 しかし， WBA で見ているのは， 放射能ではなく凍結乾燥切片表面におけるβ粒子束密度である。 しばしば"quantitative WBA"というタイトルを見かけるが， 図 9 からわかるように 14Cβ線は著しい自己吸収を受け， しかもその度合いは臓器ごとに著しく異なるのでこれを補正しない限り， quantitative というのは誤りである。 WBA の分野において RLG は特に大きな期待をもって迎えられたが， WBA 切片上の各臓器の厚さ （mgcm2） を求める方法がなかったので fs,ab を補正することができず， したがって依然として WBA の定量はできなかった。

拡大	図 9　14Cβ線の自己吸収曲線

3.1.　定量 WBA の提案

著者は WBA 切片各臓器の厚さを 147Pm 平面線源によるラジオグラフィで求め， 自己吸収を補正して WBA 切片各臓器の絶対放射能を非破壊的に測定する方法を発表した16）。 図10は， 提案する厚さ測定法の原理図である15）。

凍結乾燥切片 （50μm） 上の臓器の厚さは， 臓器の比重および含水率によって異なるが， 多くの臓器は 0 - 4 mgcm2 と計算される。 また， 凍結切片は粘着テープ （6 mgcm2 前後） の上に張り付けられ， 薄いプラスチック膜 （0.5mgcm2） を介して IP に露光される。 平面線源は， 汚染防止のためにプラスチックフィルム （2 mgcm2） でラップしなければならない。 これらを合計すると， 平面線源の RI 層と IP の間には， 約 10 mgcm2 の風袋と 0 - 4 mgcm2 の測定対象物が置かれることになる。

厚さ測定に用いられる 線源核種として 14C, 85Kr, 147Pm, 90Sr-90Y および 204Tl などがある17）。 これらのうち， 85Kr は希ガス元素であるので面線源を作ることができない。 90Sr-90Y および 204Tl はβ線のエネルギーが高すぎるので， 0 - 4 mgcm2 の厚さの差を画像として捉えることはできない。 また， 14C のβ線のエネルギーは低すぎるほか， 半減期が長いのでβ粒子束密度の高い平面線源を作ることができない。 これに対して， 147Pm は好適なエネルギー （半価層： 4 mgcm2） のβ粒子を放射し， その半減期は短いので β粒子束密度の高い平面線源を作製できる。 このような理由から， 147Pm は WBA 切片のラジオグラフィに使用できる唯一の核種であると結論した。 唯一の懸念は WBA 切片上の 14Cβ線の貢献である。 この問題は， 切片を裏返して露光すること （14Cβ線は粘着テープによってほとんどすべて吸収されしまう， 図 1 参照）， および 147Pm 平面線源の表面β粒子束密度が桁違いに高いので厚さ測定の露光時間 （30分） を WBA （数日） に比べて著しく短くできることによって解決できた。

3.2.　定量 WBA 実験例

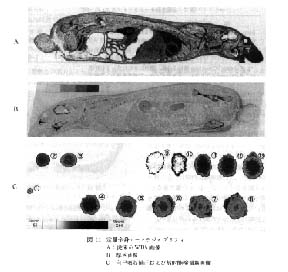
ラットに［14C］sucrose を投与し， 30， 60 （3 枚） および 90μm 切片を作製した。 図11 A は従来の WBA 画像， B は厚さ画像， C は自己吸収補正曲線および放射能検量線の作製のためにおいた試料の画像である。 A, B の画像が左右対称になっているのは， 厚さ画像は切片を裏返しにしてとっているためである。

図11 B の左上にある長方形の像は， アルミニウム箔を重ねて作製した厚さ校正切片の画像である。 この場合， アルミ箔の厚さ （mgcm2） と log PSL は優れた直線関係にあり， この検量線を使って各臓器の厚さは精確に求めることができる。

図11 C 中の ① - ⑧ は自己吸収補正曲線の作製のためのスポットである。 ① - ④ は， いずれも 14C 10 Bq をプラスチック （乾燥時の厚さ 0 mgcm2）， ろ紙 （8.0 mgcm2）， 障子紙 （6.5 mgcm2）， tissue paper （1.4mgcm2） に取り， 乾燥して得られたスポットである。 ④ - ⑧ は 14C 10 Bq を tsissue paper にとり， 乾燥した後， スポットの中心が同じ位置に来るように 1 （トータルで， 1.4 mgcm2） - 5 枚 （7.0mgcm2） を重ね， 露光して得られた画像である。 この場合， 自己吸収補正曲線は， ①と厚さの異なる紙を使って （② - ④） も作製できるし， ①と同じ厚さの紙を重ね合わせ （④ - ⑧） てもできる。 なお， fs,ab は常数であるので， 自己吸収補正曲線はそのつど作製する必要はない。
図11 C 中の ⑨ - ⑬ は 14C を tissue paper にとり作製した標準試料の画像である。 tissue paper で自己吸収補正曲線や検量線を作成する方法は， tissue paper の厚さは WBA の切片の各臓器の厚さとほぼ同じである （図 9）， すなわち自己吸収がほぼ同じであること， および自分の液シンで校正されていることの二つの理由で， 市販の標準線源を使う方法に比べて本質的に優れていると言える。

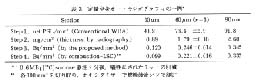
表 3 は， 肝臓について実験結果をまとめたものである。 従来の方法で得られる （PSLOB－PSLBG）mm2 （Step 1） は切片厚さに比例していない。 これは自己吸収のためである。 それに対して， 147Pm 平面線源によるラジオグラフィで求めた厚さ （Step 2） から算出した fs, ab で補正して求めた Bqmm2 （Step 3） は切片厚さに比例しており， しかもその値は， 各切片から該当部分を切り取ってオキシダイザーで燃焼し， 液シンで計数した値 （Step 4） とよく一致している。 これらの実験結果は， 自己吸収が精確に補正され， 絶対測定ができていることを示唆し， さらに"自前の標準線源"を使ったことの御利益でもある。

この方法の優れている点は， わざわざ 147Pm 平面線源を設備しなくても， 誰でもどこからでもアクセスできることである。 すなわち， 凍結乾燥切片を載せて 147Pm 平面線源に照射した IP(147Pm irradiated IP) をカセットに納めて， 宅急便で依頼者に返送し， 依頼者が画像化・解析をするか， あるいは画像情報を記録したフロッピーディスクまたは MO を依頼者に送り， 依頼者が画像解析をすれば目的を達するからである。 前者の場合の懸念は， 147Pm irradiated IP を輸送する段階で IP に記録された画像情報が乱れるのではということであるが， これは問題にならないことは 22 で解説した。 実際， このことは同一の切片の厚さ画像の解析によって実証済みである。

3.3.　β線写真

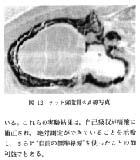
定量 WBA 開発の副産物としてβ線写真が撮れるようになったことを紹介する。 図12は， 147Pm 平面線源の上にラット WBA 切片， 普通の写真フィルムを重ねて24時間靜置した後現像して得られたラットの頭蓋骨のβ線写真で， 頭蓋骨の二重構造が素人目にもはっきり現れている。 この場合， 写真フィルムの代りに BAS 3000用 IP に露光し， 解析すれば， 画像分解能は若干悪いがより定量的な扱いが可能である。 よく知られているようにβ線の透過率は物質の種類に関係なく密度のみに依存するので， これは密度分布を正確に反映した画像である。 このようなβ線ラジオグラフィが何か新しい用途があるのではと考えている。

むす び

RLG が開発されてから10年が経過したが， 同法は放射線定量測定法としてはいまだバリデートされた方法とは言えない。 それは， 二次元放射線検出法として求められる感度および BG の面均一性試験法， 反復使用に必要な IP の RI 汚染管理法， および放射能測定法として不可欠な PSL 値の Bq 値への変換など， 最も重要な課題が未解決のままであることによる。 著者は放射化学の原点に立って， 放射線定量法として RLG を体系化し， これらの課題に対して解答を提示した。

今や14C トレーサ法は自然科学のあらゆる分野で使われている。 液シンによる 14C に対する検出限界 （10分間） はほぼ 0.1Bq である。 図 8 からわかるように， RLG によれば数 mBq まで測定できる。 このことは， 液シン廃液や少ない最大許可使用量に悩んでいる RI 関係者にとって大きな朗報である。 RLG がきわめて優れた方法でありながら， 放射線定量測定法として与えられるべき正当な市民権がいまだに与えられていないのは， 単に RLG の不幸であるばかりでなく放射化学全体の不幸でもある。 著者は， RLG が一日も早く認知され， 盛んに用いられることを願っている。

謝辞

終わりに臨み， わが国のアイソトープユーザーにとって有益な企画に取り組まれている， 栗原委員長を初めアイソトープトレーサ研究用機器専門委員の先生方に敬意を表するとともに RLG の体系化についてまとめる機会を与えていただいたことに感謝する。

一連の研究に協力された根本特殊化学ライフサイエンス研究所所員， 統計処理に貴重なご助言をいただいた新潟薬科大学宮崎　浩教授， いくつかの有益なご指摘をいただいた栗原秀員長， ならびに BAS のユーザーとして貴重なご意見を頂戴した東京薬科大学神藤平三郎教授に深甚な謝意を表する。



文献

1） 宮原諄二： 現代化学， ２２３, 29-36 （1989）
2） 森　啓司， 浜岡　勤： 蛋白質・核酸・酵素， ３９, 1877-1887 （1994）
3） Baba, S., Kimata, H., Haruki, S. and Shinohara, Y.： J. Appl. Rad. Isot., ４４, 1011-1014 （1993）
4） 日本アイソトープ協会： "アイソトープ手帳 改訂 9 版"， p. 97 （1996）
5） Baba, S., Horie, M., Asahara, N., Shiba, Y., Tomisawa, H. and Tateishi, M.,： J. Appl. Radiat. Isot., ４９, 35-39 （1998）
6） Taniyama, A., Shindo, D. and Oikawa, T.： J. Electron Microsc., ４５, 232-235 （1996）
7） 日本アイソトープ協会： "アイソトープ手帳改訂 9 版"， p. 5 （1996）
8） Baba, S., Asahara, N., Iida, S., Tomisawa, H., Tateishi, M. and Miyazaki, H.： Xenob. Metab. Disp., １３, 566-571 （1998）
9） 馬場茂雄： 薬物動態， ９, 379-385 （1994）
10） 森　啓司： Radioisotopes, ４８, 48-62 （1999）
11） 田中高彬； JAERI-M 90-049 日本原子力研究所 （1990）
12） Nakajima, E.： Radioisotopes, ４２, 22-30 （1993）
13） Nagatsuka, S., Hanawa, S., Honda, T. and Hasegawa, M.： Xenob. Metab. Disp., ３, 121 （1988）
14） 長塚伸一郎： Radioisotopes, ４８, 132-145 （1999）
15） Baba, S., Kimata, H. and Matsuzawa, T.： J. Appl. Radiat. Isot., ４８, 953-957 （1997）
16） Baba, S., Kimata, H. and Matsuzawa, T.： A quantitative whole body autoradiography. Proceedings of Synthesis and Applications of Isotopically Labelled Compounds, edited by J. Allen, Strasburg, France, 20-24 June 1994, pp. 843-847, John Wiley & Sons Ltd. （1995）
17） 日本アイソトープ協会： アイソトープ手帳改訂 9 版"， 106 （1996）